En el proceso de puesta a punto de modelos F2B desarrollado en la serie de notas preparadas por Paul Walker aparece un punto crítico en el cual los ajustes no dan el resultado esperado. Vamos a repasar brevemente lo expuesto.
Se trata del momento en que el modelo no gira igual en ambos sentidos (normal e invertido). Muchas veces el ajuste de la manija es el culpable. Es hora de revisar la manija. Si las esquinas interiores son más rápidas que las esquinas exteriores, entonces hay que acortar la línea del comando hacia abajo y volver a intentarlo. A la inversa, si los giros exteriores son más rápidos, acortar la línea del comando ascendente y volver a probar. Si esto no resuelve el problema, hay que evaluar el sesgo de la manija.
En la manija sin sesgo la línea ascendente y la línea descendente reciben un espaciamiento uniforme sobre la mano y entregan comandos balanceados al modelo. Sin embargo, también cabe considerar la opción de una manija sesgada, la cual proporciona más comando hacia abajo, y menos hacia arriba, lo que ayuda a un modelo que es demasiado rápido en las esquinas interiores.
Se prueba este cambio y se vuelve a evaluar. El ajuste del neutro de la manija y el sesgo son factores que pueden terminar actuando en conjunto y uno compensar al otro. Paul Walker sugiere que el sesgo sea ajustado a la posición neutral antes de volver a ajustar el neutro. Después de alcanzar este punto, si el modelo todavía no gira igual en ambos sentidos, la geometría básica del sistema de control debe ser considerada. Entonces esto ya dejó de formar parte del proceso de puesta a punto.
La técnica antigua era que los cuernos de flaps y elevadores se orientaban verticalmente. Si bien esto es fácil de ver y alinear, no proporciona una respuesta lineal con respecto a la rotación del balancín. Esto puede causar diferencias entre las velocidades de los giros interiores y exteriores, que pueden ser difíciles de resolver. ¿Cual es la geometría correcta para proporcionar una respuesta lineal? Hay muchas variables y no hay respuestas "simples" a esa pregunta.
Debido a esto el especialista americano Howard Rush desarrolló un programa soportado en Excel, que se muestra haciendo click en la imagen de abajo, el cual ejecuta precisamente esa tarea, quienes deseen conectarse con él para realizar comentarios o aclaraciones sobre esta herramienta pueden enviarle un correo electrónico a: athmrush@comcast.net
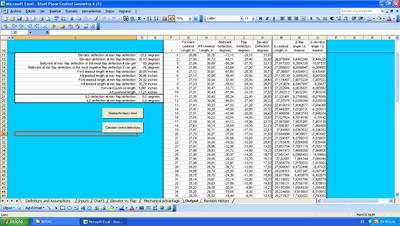
Click en la imagen para abrir el libro Excel |
Paul Walker lo ha utilizado para desarrollar la geometría del sistema no lineal en su modelo “Predator”. Tiene dos opciones, una para un sistema lineal estándar y otro para el sistema no lineal tipo Igor Burger. (Ver: “Diagramas”).
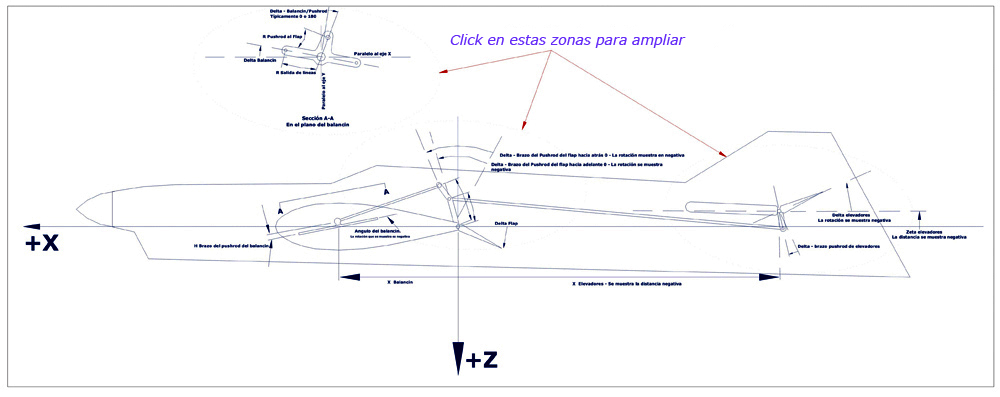
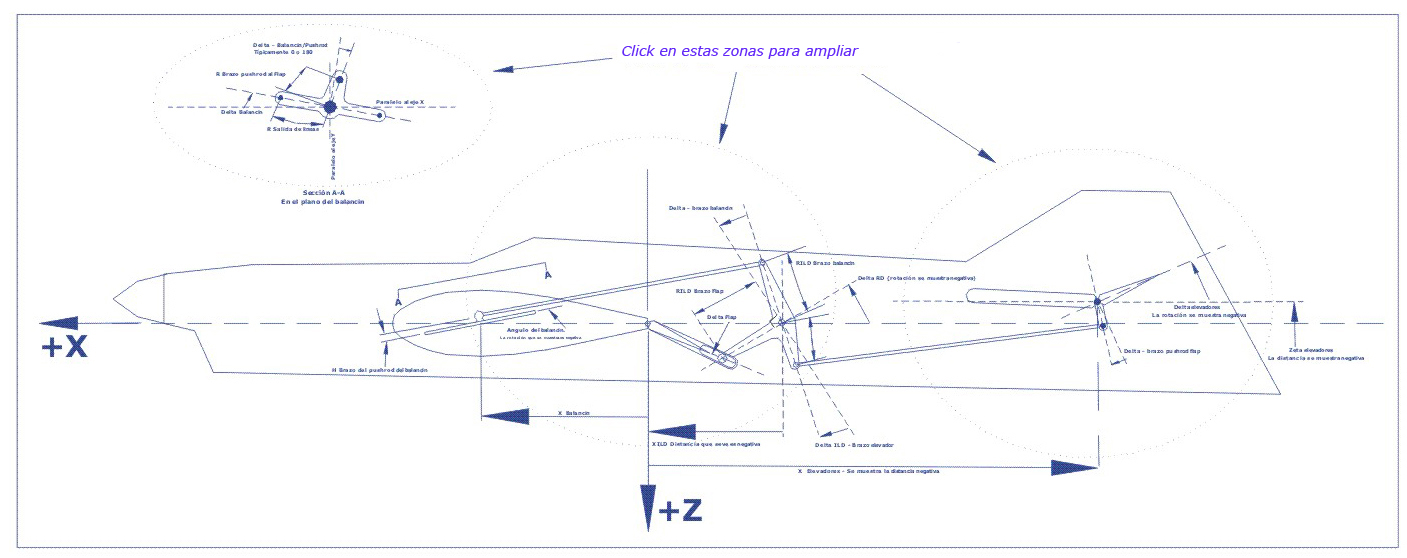
Desafortunadamente, cuando el fuselaje de un acrobático ya está completamente construido, es casi imposible resolver este tema. P.W. recomienda utilizar el programa antes de construir ya que esto no se puede resolver durante la puesta a punto, que es posterior, sino que es un ítem a considerar durante las instancias previas al inicio de la construcción del modelo.
Para usar el programa hay que variar los parámetros de entrada hasta llegar a obtener una respuesta lineal entre el recorrido de los cables de salida y la deflexión de las superficies de control. El programa supone que los agujeros en la puntera para los cables de salida y el orificio del eje del balancín están en línea.
Ponemos entonces este instrumento a disposición de los especialistas en el diseño y construcción de modelos acrobáticos para su utilización y evaluación. Las conclusiones a las que ellos arriben luego de haberlo puesto en práctica con ejemplos reales serán debidamente apreciadas por la comunidad aeromodelística.
Para finalizar quiero agradecer a Ricardo Arrayet su colaboración en la preparación de esta nota y también aprovecho para enviar a los lectores mis mejores deseos para estas fiestas y el próximo año.